Взаимодействие между 2D и 3D решателями в параметрическом ядре C3D Solver

Поводом для данной статьи послужил вопрос одного из наших заказчиков на конференции C3Days о том, как можно было бы совместно использовать 2D и 3D решатели в своём приложении и в каких случаях такое совмещение вообще может быть уместно?

Для ответа на него рассмотрим совместное использование 2D и 3D решателей на примере создания упрощённой параметрической модели многоэтажного типового здания. Пример полностью придуман и не имеет ничего общего с проектированием реального здания, зато наглядно демонстрирует один из способов организации взаимодействия между 2D и 3D решателями в клиентском приложении.

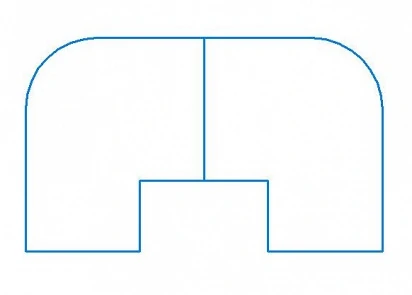
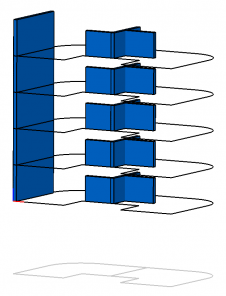
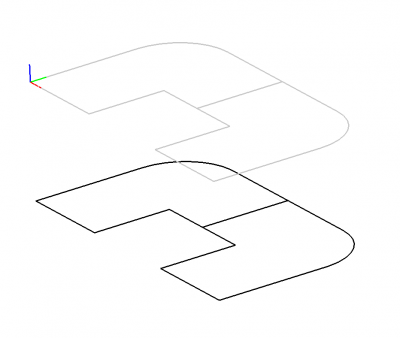
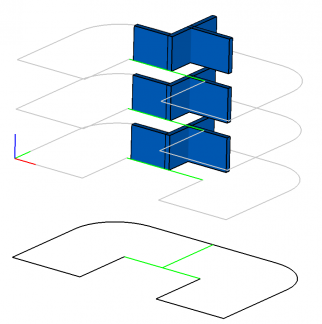
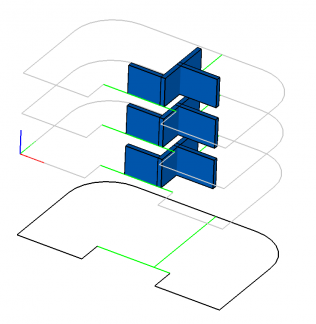
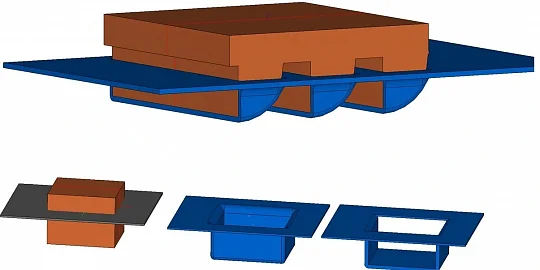
Пусть у нас есть двумерный эскиз (Рис.0.а), задающий план квартир на этаже. С его помощью мы построим трёхмерное полностью параметрическое здание (Рис.0.б) и покажем, как можно манипулировать любыми его частями с сохранением всех трёхмерных ограничений, наложенных на элементы конструкции.

Рис.0.а

Рис.0.б

Элементы

Сначала подготовим «кирпичики», из которых будет состоять наше здание. Обычно в клиентском приложении для работы с геометрическими объектами (кривыми, поверхностями, телами и т.п.) при решении задач, порождаемых предметной областью приложения (например, для визуализации), используется своё внутреннее представление геометрических объектов, наиболее подходящее к его предметной области. Такое внутреннее представление геометрических объектов мы далее будем называть клиентским или модельным. Для работы с решателем геометрических ограничений требуется отобразить клиентские геометрические объекты в предметную область решателя геометрических ограничений. Такое представление мы будем называть параметризованным представлением геометрических объектов.

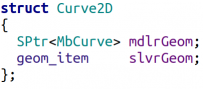
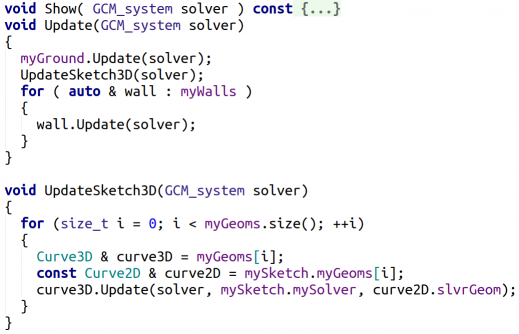
Для создания 2D-эскиза мы будем использовать двумерные кривые MbCurve из C3D Modeler. В нашем примере это будут дуги окружностей и отрезки. Чтобы получить параметризованное представление кривой, её необходимо зарегистрировать в C3D Solver с помощью соответствующих вызовов API решателя. Для агрегации этих двух представлений одной и той же кривой заведём класс Curve2D. Важно отметить, что клиентское и параметризованное представления кривой независимы друг от друга, поэтому требуется синхронизировать их между собой, для чего мы будем использовать метод Update: после изменений в эскизе будем запрашивать у 2D решателя новое положение кривых и обновлять их клиентское представление. Пример реализации метода Update для обновления состояния клиентского отрезка дан на Рис. 2

Аналогичным образом определим базовый трёхмерный объект нашей модели. Пусть это будет обычный прямоугольный блок (или, выражаясь языком математики, параллелепипед). Для клиентского представления блока мы будем использовать обычное твёрдое тело (MbSolid) из C3D Modeler, помещённое во вставку (MbInstance), чтобы через локальную систему координат (далее ЛСК) (MbPlacement3D) вставки управлять положением блока в пространстве.

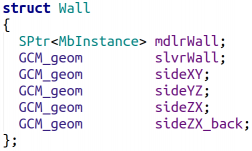
Т. к. в основном мы будем накладывать ограничения не на блок целиком, а на отдельные его грани, то также зарегистрируем в решателе и некоторые грани блока, указав при этом решателю, что они являются не независимыми друг от друга плоскостями, а частями более общего родительского объекта. В 3D решателе для этого есть специальная функция GCM_SubGeom. Иными словами, мы регистрируем плоскость в 3D решателе как подобъект некоторого родительского блока (параллелепипеда), жёстко закрепив её тем самым в системе координат данного блока. Это значит, что она сможет свободно перемещаться в пространстве, но таким образом, чтобы её положение в системе координат её родительского блока оставалось константным. Для агрегации клиентского представления блока и его параметризованного представления, которое включает и грани блока, в 3D решателе создадим класс Wall (Рис.3)

Синхронизация блока происходит элементарно (Рис.4): надо запросить у 3D решателя обновлённую ЛСК родительского объекта в глобальной системе координат (ГСК) и приписать это новое положение в пространстве вставке (MbInstance), отвечающей за клиентское представление блока.

Т. к. вспомогательные грани были определены как подобъекты блока, то их положением управлять не надо: обновлённая ЛСК блока однозначно определяет положение в пространстве и подчинённых ему плоскостей.

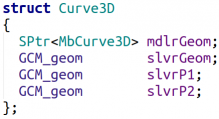
Таким образом мы определили элементарные кирпичики для построения «чистых» 2D и 3D элементов нашей модели. Теперь определим кирпичик, который будет связующим звеном между полностью независимыми друг от друга 2D и 3D объектами, управляемыми соответственно 2D и 3D решателями. В качестве такого связующего звена будем использовать трёхмерные кривые, которые будут отображением двумерных кривых, управляемых 2D решателем, в трёхмерное пространство. При этом сами отображаемые кривые всегда будут принадлежать какой-нибудь трёхмерной плоскости, на которую и будет делаться отображение. Для работы с этими кривыми на стороне клиентского приложения будем использовать трёхмерные кривые (MbCurve3D) из C3D Modeler, а на стороне решателя — неограниченные 3D кривые (в нашем примере это будут окружности и прямые) и две точки, задающие концы этих кривых (Рис.5). Класс, агрегирующий эти представления кривой, назовём Curve3D.

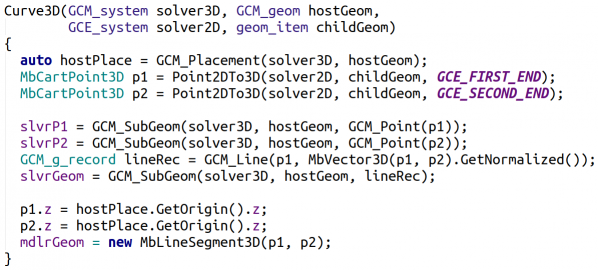
На Рис.6 показано, как примерно мог бы выглядеть конструктор, отображающий двумерный отрезок в трёхмерный. На вход в такой конструктор подаётся ЛСК этажа (hostGeom), в плоскости Oxy которой будет лежать отображаемая кривая и сама отображаемая двумерная кривая (childGeom), а также 3D и 2D системы ограничений, управляющие соответственно плоскостью и кривой. Запросив у 2D решателя координаты отрезка, мы регистрируем его как суб-объект родительской плоскости.

Важным моментом, заметно отличающим данный элемент нашей модели от предыдущих, является его синхронизация с представлением, отвечающим за визуализацию (MbCurve3D). Т. к. трёхмерная кривая управляется её двумерным аналогом, то вначале нам требуется обновить координаты двумерного объекта, что будет новым положением объекта в ЛСК его родительской плоскости, потом вычислить его новое положение в пространстве и задать в решателе новое положение трёхмерного объекта. И только после этого надо обновить клиентское представление кривой (mdlrGeom). Примерный код обновления клиентского представления отрезка представлен на Рис.6.а

Итак, у нас теперь есть три элементарных кирпичика, из которых мы будем строить наше здание: двумерные кривые (Curve2D), трёхмерный блок-стена (Wall) и трёхмерные кривые (Curve3D). При этом поведением двумерных кривых управляет 2D решатель, поведением трёхмерных тел управляет 3D решатель, а поведением трёхмерных кривых управляют сразу оба решателя: 2D решатель через управление положением кривых в ЛСК родительских плоскостей, а 3D решатель через ориентацию в пространстве родительской плоскости, на которой располагаются кривые.

Теперь, из описанных выше кирпичей, мы можем начать строить здание. Начнём с плана этажа.

Создание плана этажа

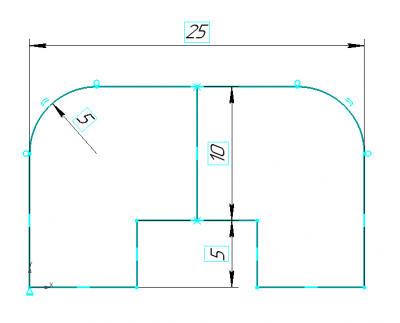
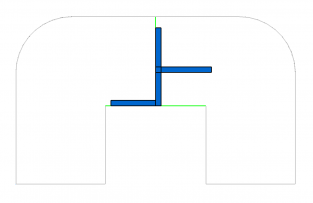
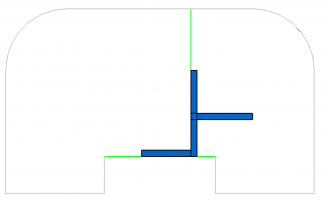
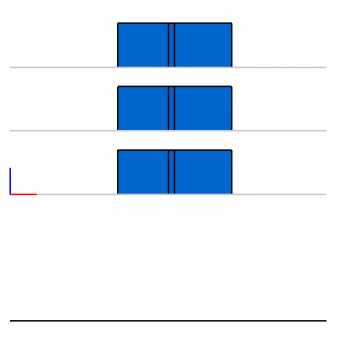
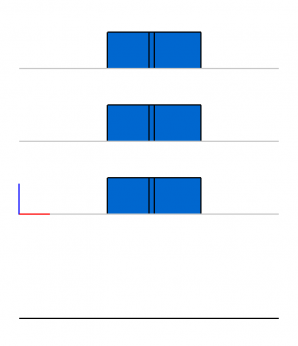
Для построения нашего многоэтажного здания нам понадобится типовой шаблон плана расположения квартир на этажах. За основу возьмём план двухквартирного этажа, изображённый на Рис.7.

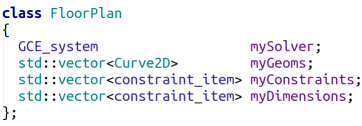
Для создания подобного эскиза заведём класс FloorPlan, который будет агрегировать в себе двумерную систему ограничений (mySolver), двумерные кривые (myGeoms) и логические (myConstraints) и размерные (myDimensions) ограничения, наложенные на кривые. Размерные ограничения мы будем использовать как элементы управления планом этажа.

Для отображения эскиза в редакторе нам понадобится ещё одно поле данных (myPlace) — положение эскиза в трёхмерном пространстве. Создание шаблона плана этажа, управляемого системой ограничений, происходит в конструкторе Рис.9. Детали рождения кривых и наложения на них ограничений, задающих эскиз, изображенный на Рис.7, скрыты в функции _FormulateSketchTemplate, Т. к. сами по себе они не несут большой смысловой нагрузки, в то же время, занимая немало строк кода. Заметим, что Т. к. план этажа рождает в конструкторе систему ограничений, которой он и владеет, то при реализации деструктора надо не забыть её удалить во избежание утечек памяти

Интерфейс класса, который понадобится нам для работы с эскизом, будет состоять из четырёх методов. Во-первых, это функция Show, отвечающая за отображение плана этажа на экране (её реализация не представляет интереса для рассматриваемой нами задачи и потому будет опущена). Во-вторых, это функция Update: после манипуляций с эскизом нам надо решить систему ограничений и, если решение прошло успешно, обновить положение всех отображаемых кривых в соответствии с их новым положением в решателе (Рис.10). В-третьих, это будут две функции для манипуляции перегородкой между двумя квартирами в нашем шаблонном плане: ChangeDimension — для изменения размера перегородки и MoveSeparator — для перемещения перегородки. Реализация этих двух функций элементарна и заключается в простом перенаправлении к соответствующим вызовам API решателя (Рис.10).

Создание этажа

Перейдём теперь к созданию трёхмерной модели здания. Для этого заведём вспомогательный класс Floor, который будет отвечать за работу с каждым конкретным этажом нашего здания.

Этаж будет состоять из пола (myGround), трёхмерных стен (myWalls), которые мы будем крепить к полу, и трёхмерных кривых (myGeoms), которые являются отображением кривых из двумерного плана этажа (mySketch) на плоскость пола (myGround). Ограничения, которыми мы будем связывать трёхмерные элементы нашей конструкции, будем хранить в поле данных myConstraints. Для создания объекта класса Floor нам понадобится местоположение этажа в пространстве, система трёхмерных ограничений, с помощью которой мы будем связывать ограничениями элементы этажа, и двумерный план этажа (см. Рис.11).

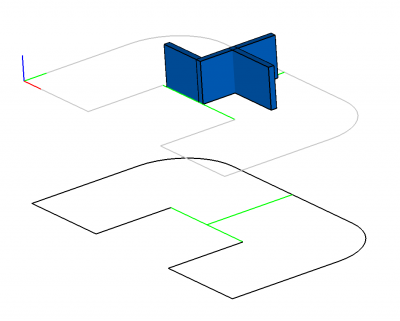
В конструкторе мы создаём все необходимые нам для работы с этажом стены, а также, пробегая в цикле по всем двумерным кривым плана этажа, создаём в плоскости пола их трёхмерные образы (Рис.12, где чёрным цветом изображён двумерный план этажа, а серым — его трёхмерное отображение в плоскость пола) и добавляем их в трёхмерную систему ограничений. К этим кривым с помощью 3D решателя мы будем крепить стены, которые условно будем дальше называть несущими. Мы будем называть такой отображённый в трёхмерное пространство двумерный план этажа трёхмерным планом этажа или трёхмерным эскизом этажа.

Детали создания стен и связывания их ограничениями скрыты в функции _FormulateWalls, Т. к. они не имеют прямого отношения к теме статьи. Отметим лишь, что условно все ограничения, накладываемые на элементы конструкции этажа, можно разделить на три типа. Во-первых, это крепление тел к полу наложением ограничения «Совпадение плоскостей» между полом и крепимой к полу гранью стенки. Во-вторых, это ограничения между самими стенами, которые будут задавать, например, компоновку комнат внутри квартиры. Такая компоновка может быть индивидуальна для каждого этажа. И, в-третьих, это ограничения, привязывающие несущие стены к трёхмерным кривым, задающим план-эскиз этажа. Примеры задания всех этих трёх видов ограничений приведены на Рис.13.

В итоге мы получим этаж примерно такого вида, как изображен на Рис.14 (для простоты восприятия тут и далее мы не будем перегружать нашу конструкцию большим числом лишних элементов, отображая лишь минимально необходимый их набор): все синие стенки и трёхмерный план (серые и светло-зелёные кривые) лежат на плоскости пола (myGround), все стенки соединены между собой ограничениями «Совпадение плоскостей» и одна стенка (несущая стена) жёстко привязана к трёхмерной кривой (перегородке между «квартирами») трёхмерного плана.

Интерфейс класса Floor по аналогии с классом FloorPlan содержит метод визуализации этажа Show и метод Update для обновления всех элементов конструкции этажа (стен и 3D кривых) по их состоянию в 3D и 2D решателях (Рис.15). Обновление трёхмерного плана этажа было вынесено в отдельную функцию UpdateSketch3D по причинам, которые станут ясны позже.

Создание здания

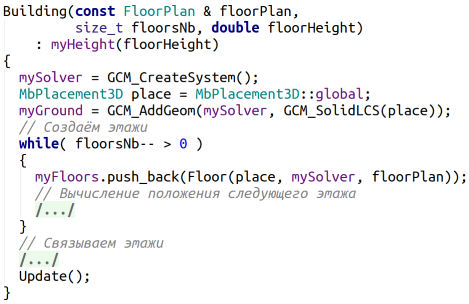
После того как мы определи класс Floor, можем перейти к созданию полностью параметризованного многоэтажного здания. Заведём для этого класс Building (Рис.16). Так же, как двумерный эскиз FloorPlan владел двумерной системой ограничений, класс Building будет владеть трёхмерной системой ограничений (mySolver). Наше здание будет иметь нулевой уровень (myGround), состоять из массива этажей (myFloors), имеющих для простоты одинаковую высоту (myHeight). Ограничения между этажами будем хранить в поле данных myConstraints.

В конструкторе дадим возможность задать число этажей в здании, высоту этажей и их двумерный план расположения квартир (Рис.17).

Из тонкостей реализации конструктора отметим связывание всех этажей здания в линейный массив компонент (GCM_LINEAR_PATTERN), который управляет согласованным положением всех этажей при различных манипуляциях с ними: все они будут расположены вдоль оси Oz нулевого уровня (myGround), а ЛСК плоскостей их полов будут параллельны и выровнены по осям Ox и Oy с ЛСК нулевого уровня.

Т. к. класс Building владеет трёхмерной системой ограничений, не забудем удалить её в деструкторе во избежание утечки памяти (Рис.19).

Так же, как и классы FloorPlan и Floor, класс Building будет иметь методы Show и Update (Рис.20). Важным моментом в реализации данного метода является необходимость двукратного обновления состояния кривых, образующих трёхмерные планы этажей. Поскольку трехмерные кривые в нашей задаче управляются также и 2D решателем, то перед тем, как решить трехмерную систему ограничений, мы должны вначале запросить у 2D решателя актуальные положения кривых в ЛСК плоскостей, суб-объектами которых они являются. После этого решим трехмерную систему ограничений и обновим положения всех этажей. При обновлении этажа кривые, образующие трёхмерный план этажа, будут обновлены повторно, отражая уже результат работы 3D решателя.

Кроме того, для демонстрации работы параметризации между этажами здания добавим метод ChangeFloorHeight, который позволит изменять высоту этажей (Рис.21). Когда мы связали в конструкторе все этажи здания в линейный массив компонент с константным шагом, равным высоте этажей, то в терминах C3D Solver мы фактически создали набор управляющих линейных размеров, равных расстояниям между плоскостью нулевого уровня (myGround) и плоскостью пола этажа. Поэтому для изменения высоты этажей мы воспользуемся функционалом, предусмотренным в API 3D решателя для изменения величины управляющего размера, — GCM_ChangeDrivingDimension.

Работа со зданием

Описав класс Building, посмотрим теперь, как с помощью него и плана этажа FloorPlan можно создать параметризованное трёхмерное здание и управлять его видом.

На Рис.22 представлен пример кода, где мы сначала создаём здание: шаблон трёхэтажного здания по заданной двумерной планировке квартир на этажах с высотой этажей равной 5 занимает всего две строчки кода. Рис. 23.а, Рис.24.а и Рис.25.а показывают созданное здание в разных проекциях. После, редактируя двумерный план расположения квартир на этажах, меняем сначала размер перегородки между квартирами, а потом сдвигаем перегородку немного вправо, делая тем самым площадь левой квартиры больше. И в конце изменяем высоту этажей с 5 на 7. После этого, чтобы применить сделанные изменения, нам остаётся обновить состояния двумерного плана и здания, решив 2D и 3D системы ограничений вызовом метода Update поочерёдно у двумерного эскиза и здания. Результат внесенных изменений в разных проекциях показан на Рис.23.б, Рис.24.б, Рис.25.б. Как видно из полученных результатов, благодаря 2D и 3D решателям нам не требуется заботиться о выполнении наложенных на объекты нашей модели двумерных и трёхмерных взаимосвязях (ограничениях), после манипуляций над элементами управления — все двумерные и трёхмерные ограничения выполняются автоматически. Всё, что нам потребовалось — это обеспечить синхронизацию передачи данных от 2D эскиза в 3D решатель, отвечающий за параметризацию здания.

Рис.23.а

Рис.23.б

Рис.24.а

Рис.24.б

Рис.25.а

Рис.25.б

Выводы

В результате мы создали параметризованную модель типового многоэтажного здания, которую можно редактировать, не заботясь о поддержании связей (геометрических ограничений), между элементами его конструкции — за это отвечают 2D и 3D решатели. Единственные наши накладные расходы — забота о синхронизации данных между 2D и 3D решателями. В то же время совместное использование 2D и 3D решателей, как видно из рассмотренного примера, может дать ряд плюсов.

Во-первых, за счёт переноса ответственности за поддержание связей между трёхмерными кривыми на 2D решатель, мы получаем намного более компактную систему уравнений в 3D решателе, что заметно повышает стабильность её решения и увеличивает производительность нашей программы в целом.

Во-вторых, у нас получилась хорошо масштабируемая задача. Т. к. план любого этажа управляется одним и тем же двумерным эскизом, т.е. одной и той же системой уравнений, нам не требуется при конструировании каждого нового этажа создавать большое число одних и тех же ограничений, задающих трёхмерных эскиз-план этажа по-отдельности. По этим же причинам мы избавлены от необходимости связывать между собой ограничениями элементы конструкции с разных этажей, чтобы обеспечить их согласованное поведение. Например, в рассмотренной задаче это было использовано нами для согласованного редактирования перегородки между квартирами (несущей стены) одновременно на всех этажах.

В-третьих, такой подход позволяет накладывать на трёхмерные кривые ограничения, которые в настоящий момент не поддерживаются 3D решателем, при условии, что они исполняются в какой-нибудь плоскости. Например, размерное ограничение между двумя трёхмерными окружностями, лежащими в одной плоскости.